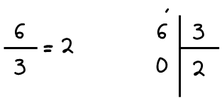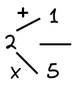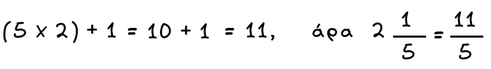KAΛΑ ΧΡΙΣΤΟΥΓΕΝΝΑ

Έργο  του  Γ2΄ τμήματος  (Δασκάλα: κ. Λίνα Παρικίδου)

 Οι μαθητές και οι εκπαιδευτικοί του Ε2΄ τμήματος σας εύχονται  ολόψυχα:

"ΚΑΛΑ  ΧΡΙΣΤΟΥΓΕΝΝΑ, ΧΡΟΝΙΑ ΠΟΛΛΑ  ΚΑΙ  ΚΑΛΗ ΧΡΟΝΙΑ !!!

ΜΕΤΑΤΡΟΠΗ ΚΛΑΣΜΑΤΟΣ ΣΕ ΜΕΙΚΤΟ ΑΡΙΘΜΟ & ΤΟ ΑΝΤΙΣΤΡΟΦΟ

Aναδημοσίευση από: e-class 31ο δημοτικό σχολείο Περιστερίου

---

Για να μετατρέψουμε γρήγορα ένα κλάσμα (καταχρηστικό) σε μεικτό αριθμό...

---

1. Διαιρούμε τον αριθμητή με τον παρονομαστή.

2. Το πηλίκο της διαίρεσης είναι ο ακέραιος του μεικτού.

3. Το κλάσμα του μεικτού έχει αριθμητή το υπόλοιπο της διαίρεσης και παρονομαστή τον ίδιο με το αρχικό κλάσμα.

---

Παράδειγμα

---

Αν διαιρέσουμε τους όρους ενός καταχρηστικού κλάσματος, θα μας προκύψει ή ακέραιος ή μεικτός αριθμός.

ακέραιος

μεικτός

---

---

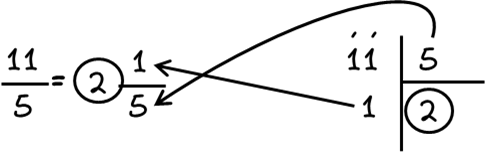
Για να μετατρέψουμε γρήγορα ένα μεικτό αριθμό σε κλάσμα...

---

1. Πολλαπλασιάζουμε τον ακέραιο του μεικτού με τον παρονομαστή του κλάσματός του.

2. Στο γινόμενο που προκύπτει προσθέτουμε τον αριθμητή του μεικτού αριθμού.

3. Το αποτέλεσμα αποτελεί τον αριθμητή του νέου κλάσματος, ενώ παρονομαστής παραμένει ο ίδιος.

---

Παράδειγμα

Oι τρεις μουσικοί

Στα πλαίσια του  μαθήματος της Γλώσσας (ασκ. 2 /σελ. 20 ΒΜ β΄τεύχος)  σας παρουσιάζουμε το  ποίημα  το οποίο  γράψαμε στην τάξη  μας:

                                      

                                               ΟΙ   ΤΡΕΙΣ  ΜΟΥΣΙΚΟΙ

                                               Τρεις  μουσικοί

                                               με άρπα, κιθάρα και βιολί,

                                               παίζαν΄ ωραία  μουσική

                                               επάνω στη  σκηνή.

                                               Κόσμος   ερχόταν  να τους  δει

                                               κι αυτοί χαιρόντουσαν πολύ

                                               χορούς, τραγούδια και χαρά,

                                               γέμισε όλ΄  η γειτονιά!

Πώς μεγαλώνω ένα κλάσμα, το μικραίνω ή φτιάχνω ισοδύναμά του.

Αναδημοσίευση από:  ΠΑΡΑ-ΜΟΡΦΩΣΗ

Πώς μεγαλώνω ένα κλάσμα, το μικραίνω ή φτιάχνω ισοδύναμά του.

                                                                              Οδηγίες: 

• Πατάμε στον παραπάνω σύνδεσμο και μεταβαίνουμε στον ιστότοπο με την παρουσίαση.
• Για να τρέξει  η παρουσίαση  κάνουμε- με το ποντίκι μας- αριστερό κλικ  επάνω της.
• Κάνουμε το ίδιο και για να προχωρήσουμε στις επόμενες  σελίδες της παρουσίασης.

ΠΩΣ ΜΕΓΑΛΩΝΩ & ΜΙΚΡΑΙΝΩ ΕΝΑ ΚΛΑΣΜΑ

Αναδημοσίευση από :  Δια...δικτύου μάθηση  e-class
                                   31ο Δημοτικό σχολείο Περιστερίου

Για να μεγαλώσω ένα κλάσμα...

• πολλαπλασιάζω τον αριθμητή του κλάσματος  με έναν αριθμό (όσες φορές θέλω να το μεγαλώσω) ή
• διαιρώ τον παρονομαστή του κλάσματος με έναν αριθμό (όσες φορές θέλω να το μεγαλώσω).

Παράδειγμα



Για να μικρύνω ένα κλάσμα...

• διαιρώ τον αριθμητή του κλάσματος  με έναν αριθμό (όσες φορές θέλω να το μικρύνω) ή
• πολλαπλασιάζω τον παρονομαστή του κλάσματος με έναν αριθμό (όσες φορές θέλω να το μικρύνω).

Παράδειγμα

Ισοδύναμα κλάσματα

 

  Παρουσίαση για τα  ΙΣΟΔΥΝΑΜΑ  ΚΛΑΣΜΑΤΑ

                                                                 του  Γιάννη Φερεντίνου

Επίσκεψη στο Βυζαντινό Μουσείο Θεσσαλονίκης

Την  Πέμπτη, 26 Νοεμβρίου 2015, το τμήμα μας (Ε2΄) , μαζί με τα  Ε1΄και Στ'  τμήματα  είχαμε την τύχη να επισκεφτούμε το Βυζαντινό Μουσείο της πόλης μας.

Η περιήγηση στο μουσείο , υπό την καθοδήγηση ξεναγού ήταν πολύ  ενδιαφέρουσα  κι  επικοδομητική  για τους μαθητές και τις μαθήτριές μας, ειδικά για τα ...πεμπτάκια μας , που διδάσκονται φέτος την ιστορία του Βυζαντίου.Ακολουθούν κι άλλες   φωτογραφίες απ΄ το Μουσείο

.

Τα κλασματα

ΑΝΑΔΗΜΟΣΙΕΥΣΗ από:

  δασκάλα ΒΜ Ιστολόγιο για την πέμπτη τάξη

                                                       Τα κλασματα

1.   Το κλάσμα εκφράζει το ακριβές πηλίκο μιας διαίρεσης: της διαίρεσης του αριθμητή με τον παρονομαστή του κλάσματος

              6  = 6 : 7

7

2.   Οι δεκαδικοί αριθμοί γράφονται και ως δεκαδικά κλάσματα

0,5=  5        0,23=  23

        10                 100

3.           Αφού κάθε κλάσμα είναι μία διαίρεση, μετατρέπω  ένα κλάσμα σε δεκαδικό αριθμό αν διαιρέσω τον αριθμητή  με τον παρονομαστή .

 

4.   Δύο ή περισσότερα κλάσματα λέγονται ισοδύναμα ή ίσα όταν έχουν την ίδια  αξία αλλά διαφορετικούς όρους . 

 

5.   Για να φτιάξω ισοδύναμα κλάσματα με ένα αρχικό κλάσμα , πολλαπλασιάζω ή διαιρώ αριθμητή και παρονομαστή με τον ΙΔΙΟ αριθμό.

 

6.   Για να απλοποιήσω ένα κλάσμα ΔΙΑΙΡΩ τον αριθμητή και τον παρονομαστή του με τον  ΙΔΙΟ αριθμό

 

7.   Ανάγωγο λέμε το κλάσμα που δεν απλοποιείται άλλο. πχ

 

8.   Ένας τρόπος για να βρω ποιος αριθμός διαιρεί τον αριθμητή και τον παρανομαστή ενός κλάσματος, δηλαδή για να το απλοποιήσω, είναι  να βρω το ΜΚΔ τους.

9.   Ένα κλάμα είναι γνήσιο, είναι δηλαδή μικρότερο από το 1 όταν ο αριθμητής του είναι μικρότερος  από τον παρονομαστή του . πχ

                                                   

10.Ένα κλάσμα είναι ίσο με το 1 όταν ο αριθμητής είναι ίσος   με τον παρονομαστή του. 

 

10.        Ένα κλάσμα είναι καταχρηστικό, δηλαδή μεγαλύτερο από το 1, όταν ο αριθμητής του είναι μεγαλύτερος από τον παρονομαστή του. ΠΧ

 

                               

11.        Μεικτός λέγεται ο αριθμός που έχει και ακέραιο μέρος και κλασματικό

    

 -Μετατρέπω μεικτό σε κλάσμα: πολλαπλασιάζω τον παρονομαστή με τον ακέραιο και προσθέτω τον αριθμητή . Αυτόν τον αριθμό τον βάζω αριθμητή του νέου κλάσματος. Παρονομαστή αφήνω τον ίδιο .

 

   
 -Μετατρέπω καταχρηστικό κλάσμα σε μεικτό : Διαιρώ τον αριθμητή με τον παρονομαστή. Το πηλίκο τηε διαίρεσης είναι το ακαίρεο μέρος του μεικτού, αριθμητής του κλάσματος το υπόλοιπο και παρονομαστής  ο ίδιος (δηλ. ο διαιρέτης )

  11  = 11 :4 = 2   3   

4                       4

12.        Ομώνυμα λέγονται τα κλάσματα που έχουν τον ίδιο παρονομαστή .

 

Πώς συγκρίνω ομώνυμα κλάσματα

Ανάμεσα σε δύο ή περισσότερα ομώνυμα κλάσματα, μεγαλύτερο είναι αυτό που έχει  το μεγαλύτερο αριθμητή .

      

                                    

    

13.Ετερώνυμα λέγονται τα κλάσματα που δεν έχουν τον ίδιο παρονομαστή, αλλά διαφορετικό πχ

Πώς συγκρίνω ετερώνυμα κλάσματα

1. ετερώνυμα κλάματα  με τον ίδιο αριθμητή : Μεγαλύτερο είναι αυτό που έχει το μικρότερο  παρονομαστή.

  

 

2. ετερώνυμα κλάματα  με διαφορετικό αριθμητή :

 

Α τρόπος: Μετατρέπω τα κλάσματα σε δεκαδικούς αριθμούς

 

Β τρόπος: Μετατρέπω τα ετερώνυμα κλάσματα σε ομώνυμα

Για να μετατρέψω ετερώνυμα κλάσματα σε ομώνυμα ακολουθώ την παρακάτω διαδικασία:

α) Βρίσκω το ΕΚΠ των παρονομαστών τους       ΕΚΠ (4,6,8)= 24

β) Διαιρώ το ΕΚΠ με τον παρονομαστή κάθε κλάσματος και το πηλίκο το βάζω στο καπελάκι                 24: 4=6       24:6=4       24:8=3

γ) Πολλαπλασιάζω τους όρους (αριθμητή και παρονομαστή) κάθε κλάσματος με τον αριθμό στο καπελάκι (φτιάχνω έτσι ισοδύναμα ομώνυμα κλάσματα)

Αφού    9   <  12  <   20      ΑΡΑ     3   < 2  <  5

             24       24        24                 8      4      6 

Πρόσθεση και αφαίρεση  κλασμάτων

Για να κάνουμε πρόσθεση ή αφαίρεση κλασμάτων πρέπει να τα μετατρέψουμε πρώτα σε ομώνυμα (με τον τρόπο που περιγράψαμε παραπάνω)

1. Προσθέτω ομώνυμα κλάσματα προσθέτοντας τους αριθμητές τους .

 

Προσθέτω μεικτούς αριθμούς. Προσθέτω πρώτα το ακέραιο μέρος και μετά το κλασματικό (τα κλάσματα τα έχω κάνει ομώνυμα)

 

2. Αφαιρώ ομώνυμα κλάσματα αφαιρώντας τους αριθμητές τους

Αφαιρώ κλάσμα από ακέραιο

Μετατρέπω τον ακέραιο σε κλάσμα βάζοντας παρονομαστή το 1. 
Μετά κάνω τα κλάσματα ομώνυμα και αφαιρώ τους αριθμητές

Πολλαπλασιασμός κλασμάτων

Θυμάμαι : πολλαπλασιάζω ΠΑΝΤΑ κλάσμα με κλάσμα, τον ακέραιο ή το μεικτό 

ΠΡΕΠΕΙ να τον μετατρέψω σε κλάσμα για να τον πολλαπλασιάσω με κλάσμα. 

1.   Κλάσμα με κλάσμα

Πολλαπλασιάζω αριθμητή με αριθμητή  και παρονομαστή με παρονομαστή .

    

 

 ΠΡΟΣΟΧΗ: Δε χρειάζεται να είναι ομώνυμα.

2.   Ακέραιο με κλάσμα

Μετατρέπω τον ακέραιο σε κλάσμα βάζοντας παρονομαστή το 1.

 

3.Μεικτό με κλάσμα

Μετατρέπω το μεικτό σε κλάσμα

 

Διαίρεση κλασμάτων

Θυμάμαι ότι και στη διαίρεση ισχύει ό,τι για τον πολλαπλασιασμό.  
Μπορώ να διαιρέσω ΜΟΝΟ κλάσματα.  Μετατρέπω τον ακέραιο ή το μεικτό σε κλάσμα για να τον διαιρέσω με κλάσμα

Για να διαιρέσω κλάσματα  αντιστρέφω τους όρους του δεύτερου κλάσματος κι αντί για διαίρεση κάνω πολλαπλασιασμό